ここでは，変数
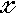と それに対応する値
（＞0） について，軸（縦軸）のみを対数目盛にしたグラフを考えます。このグラフが直線になるとき，次のような式が成り立ちます。
＝a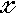＋ｂ ………[1]ただし，a，ｂ は任意の定数です。
ここで
＝
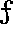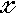（）とおくと，[1]式より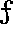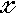（）＝a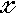＋ｂ ………[1]’また，[1]’式より
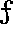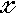（-1）＝a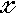（-1）＋ｂ ………[1]”[1]’- [1]”を計算すると
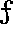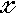（）−log10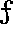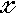（-1）＝aなので
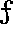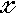（）／log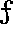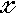（-1）｝＝aここで A＝10a とおくと，
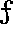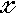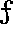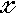（）／（-1）＝Aよって，
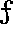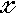（）＝A x 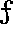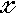（-1） ………[2]となります。
したがって，
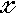の値によらず は 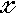が 1 増加すると A（定数）倍になります。当然のことながらこのことは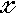， の任意の一定量の増加について成り立ちます。
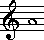なお，この種の関数の例として，音階の基本周波数があります。これは，ノートナンバー69（右図）の音の 440Hz を基準にして，ここから 1 オクターブ増減するたびに周波数が 2 倍, 1/2 倍になり，そしてその間の 12 半音の間では”増加率”が一定になっています。このことを式にすると次のようになります。周波数を
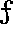[Hz]，m をノートナンバーとすると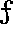，＝440 x (21/12)m - 69ただし，MIDI音源の状態によっては，基準の周波数が 440 Hz と若干ずれていることもあり得ます。