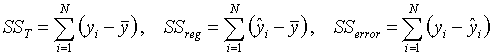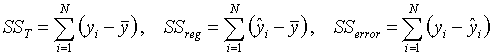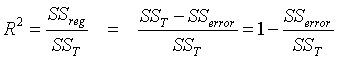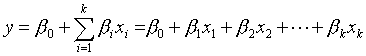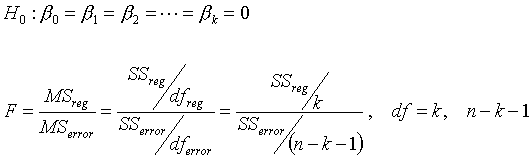重回帰分析のモデルの有意性について

• 回帰分析において、回帰モデル（回帰直線や重回帰直線）がどれだけよくデータに適合しているか、すなわち、分析に加えた説明変数（独立変数）によってどれだけよく目的変数（従属変数）が説明できるか、ということを知ることが大切になる。
• 重回帰分析の場合は、どの独立変数を分析に加え、どの独立変数を分析から除外するかに応じて、複数のモデル（重回帰式）ができる。そのなかで最適なモデルを選択するためにも「モデルの適合度」や「モデルの有意性」を調べる必要がある。
• 従属変数の説明力の強さ（当該の従属変数によって、どれだけ正確にデータを予測することができるか）はＲ²（決定係数）で表される。
• 回帰モデルの有意性はＦ検定（分散分析）で検定することができる。
• これらは独立変数の実測値（データ）と予測値（モデルによる予測値）のばらつき（２乗和）をもとに説明することができる。

■平方和

• 全体平方和：　従属変数の偏差平方和（「従属変数」と「従属変数の平均値」の差の平方和）を全体平方和（SS_T ）と呼ぶ。これは従属変数がどの程度ばらついているかの指標である。
• 回帰平方和：　「予測値」と「従属変数の平均値」の差の平方和を回帰平方和（SS_reg ）と呼ぶ。これは予測値が従属変数の周りにどのくらいばらついているかの指標である。予測値が従属変数と完全に一致するならば（＝すなわち、従属変数を独立変数の間に完全な正の相関があるならば）全体平方和と等しくなる。
• 残差平方和：　「独立変数」と「予測値」との間の差の平方和を残差平方和（SS_error ）と呼ぶ。これは予測値と従属変数との予測値とのずれを表す指標であり、いわゆる「予測の誤差」を表している。予測値が従属変数と完全に一致するならば、この値はゼロになる。
• SS_T, SS_reg, SS_errorはそれぞれ次のようになる。

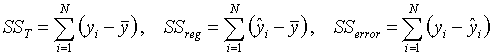
• SS_T, SS_reg, SS_errorの間には　SS_T = SS_reg + SS_error　という関係がある。

■決定係数

• 全体平方和（SS_T）の中で回帰平方和（SS_reg）の占める割合を決定係数（R²）と呼ぶ。
• 決定係数は０から１までの値をとり、回帰直線（回帰モデル）の「説明力の強さ」を表す指標である。
• 独立変数が一つの場合（単回帰）には決定係数R²は、相関係数Rの２乗と一致する

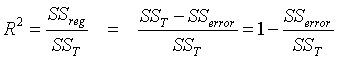
• 「予測の誤差」を示すSS_error が小さくなればなるほど、決定係数は１に近づくことが式から明らかである。

■モデルの有意性

• 回帰モデルが意味があるか否かを検定することができる。
• 次のような回帰モデルを考える。

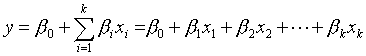
• この回帰モデルが意味があるか否かは、「全ての係数がゼロである」という帰無仮説をたてて、次のように検定（Ｆ検定：分散分析）をすることができる。

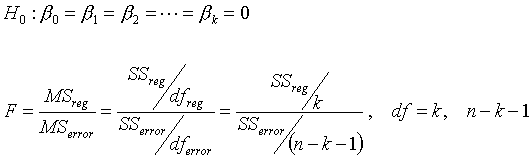
• この分散比（Ｆ）は、回帰モデルによる予測（データのばらつきとして表されている：SS_reg ）が、予測の誤差（同様にばらつきとして表されている：SS_error ）に比べてどの程度大きいかを示している。