fireb.gif はじめに 00/04/03

はじめに

またもやグラフィックエフェクトについていろいろやることにしたんですが、 ここではそんなに目新しいエフェクトをやっていくわけではありません。どれも これまでに使われたものです（多分）。今更....と思う人もいるかもしれませんが、 基礎的なエフェクトは理解すれば、自分の血となり肉となります。 そうなればどんな派手なエフェクトを作ることもできるはずです。
「一を知って十を知ることはできるが、十から一を知るのは難しい」 のです。というわけで、このコーナーではグラフィックエフェクトの 解説からサンプルまでを、 座標変換、落とし穴、高速化の三つに分けて やっていこうと思ってます。

いきなり

ですが、グラフィックエフェクトには大きく二種類あると思います。 一つは回転、テクスチャマッピングなどのような「画像の形を変化させるもの」、 一つはアルファブレンディング、色調変化などのような「画像の色を変化させるもの」です。 まずは「画像の形を変化させるもの」から見ていきます。

画像の形を変化させるということですが、 「形を変化させるには」どうすればいいのでしょうか？ 変形処理にはたいてい「座標変換」という概念がつきまとうのですが、 この概念を、「画像の拡大縮小」をとおしてみていきましょう。 もちろん、既存の関数は使いません。

まずは「一本の線」で考えてみましょう。
これが長さ10pixelだとすると、半分の長さにするにはどうしますか？ たとえば、次のような場合なら....

図-1

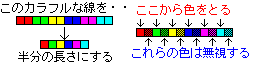
右の図のようになるのは直感的にわかるはずです。「どの色をとるか」は 左の図のとおりになっているのもわかると思います。また、黒っぽい色で示したところは 無視されていますね。結論として「１pixelとばしで色をとってきている」ということが いえます。ということは、「半分の線のX個目の点の色は、元の線のX*2個目の点の色である」 といえますよね？ここで、半分の線の座標をx'、元の線の座標をxとすると... x'=x/2が導けますね。今回の場合、 これが「座標変換関数」にあたります。 このへんでちょっとプログラムにしてみましょう。
var x:Integer;
begin
  for x:= 0 to 元の線の長さ-1 do begin
      半分の線[x/2]:=元の線[x];
  end;
end;
これは、一本の線、つまり一次元の画像を縮小するものです。 では一般的な二次元画像ではどうなるの？・・・簡単です。 横軸xについての変換に、縦軸yの変換が加わるだけです。実際に変換関数を書いてみると、 y'=y/2となります。 何が変わったかというと、先ほどでてきたxがyに変わっただけですね。 これも簡単にプログラムにできそうです。
var x,y:Integer;
begin
  for y:= 0 to 元の画像の高さ-1 do begin
      for x:= 0 to 元の画像の幅-1 do begin
          半分の画像[x/2,y/2]:=元の画像[x,y];
      end;
  end;
end;
こうなりますよね。さて、「座標変換」についてちょっとでもつかんでもらった（？） と思います。しかし、画像変形にはまだ落とし穴が待っているのです。 次は「画像変形の落とし穴」を見るために、画像を縦横２倍に拡大してみることにしましょう。

リラックス、リラックス 落とし穴にはまろう

2倍の拡大処理は次のようになります。例によって一次元からです。

図-2
先ほどとおなじように、変換関数を考えてみます。 2倍の線の座標をx'、元の線の座標をxとすると、x'=x*2となるのは 容易に想像できますね。それでは同じようにプログラムにしてみます。
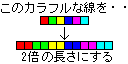
var x:Integer;
begin
  for x:= 0 to 元の線の長さ-1 do begin
      2倍の線[x*2]:=元の線[x];
  end;
end;
しかし、このプログラムで画像を拡大しようとすると、次のようになってしまいます。
図-3
このように、「穴」があいてしまうのです。これが画像変形の「落とし穴」なんです。 なんでこんなことになるのかというと、上のプログラムでは「10に5を当てはめただけ」 ですからです。10には10を当てはめないと「穴」ができるのは当然です。逆に、画像縮小プログラムでは 「5に10を積めこむ」ので、あまりはでますが「穴」はできないのです。

では「穴」があかないようにするにはどうすればいいのか？
ここは、発想の転換が必要になります。今までだと「変換前の座標から変換後の座標を求める」 という方法でしたが、これを「変換後の座標は変換前のどこにあたるかを求める」という方法にします。 これを、「逆変換」といいます。 テストに出るくらい重要なことなので、絶対に忘れないように（＝覚えておいて）しましょう。 画像変形だけでなく、プログラム全般に応用できる、偉大なる考え方です。

それでは拡大の変換関数を逆変換してみます。x'=x*2は、「x'=〜」という式ですから、これを 逆変換すると「x=〜」となるわけです。実際には、x=x'/2となりますね。 逆変換できたところで、プログラムにしてみましょう。

var x:Integer;
begin
  for x:= 0 to 2倍の線の長さ-1 do begin
      2倍の線[x]:=元の線[x/2];
  end;
end;
二次元の画像では、 
var x,y:Integer;
begin
  for y:= 0 to 2倍の画像の高さ-1 do begin
      for x:= 0 to 2倍の画像の幅-1 do begin
          2倍の画像[x,y]:=元の画像[x/2,y/2];
      end;
  end;
end;
となります。

画像変形一般

ここまで駆け足で見てきましたが、これでだいたい画像変形については終わりです。 ちょっと、画像変形に共通するプログラムを書いてみます。

var x,y,u,v:Integer;
begin
  for y:= 0 to 変形後の画像の高さ-1 do begin
      for x:= 0 to 変形後の画像の幅-1 do begin
          u=fx(x);
          v=fy(y);
          変形後の画像[x,y]:=変形前の画像[u,v];
      end;
  end;
end;
fx,fyは逆変換を行う関数です。実はこの関数の工夫次第でどんなエフェクトを作り出すことも可能です。

高速化

ここまで見てきましたが、おそらく先ほどのままのプログラムではリアルタイム（ゲーム、デモなど）で 使うには少し処理が遅いと思います。そこで、高速化の必要が出てくるわけですが、 高速化はその変形処理にあわせたものが必要なので、次回から見ていくことにします。

と、ここまで「画像変形」のみを見てきましたが、いかがでしたでしょうか？ まだまだいたらないところばかりだと思いますが、わからないところがあれば掲示板で 質問してください。






もどる