謝辞
最初に、画像回転を実装するのに非常に参考になったソースなどの 作者さんがたにお礼を申し上げます。 堀さんの「DelphiX」の「DXRender.pas」はクリッピングの参考書として 使わせていただきました。SANDMANさんの「QuadrupleD」のサンプル「hashiri」は 高速化、固定小数点の参考書として使わせていただきました。 これらのようなソースをフリーで公開していただき、どうもありがとうございました。What's 画像回転?
画像回転とは、読んで字のごとく「画像を回転させる処理」ですね(^^;)
やることと、その利点
というわけで、見た目は割と地味なんですけど、「いざ」と思ってやってみると、 手が出なかったり、うまくできなかったりするものです。また、ゲームなどで用いられる グラフィックの回転パターンをいちいち用意せずとも、プログラムで 回転させることができるというのは、大きな魅力だと思います。Direct3D IMでも こういうことが出来るわけなんですが、これには高速な「ビデオカード」が必要になります。 今の日本のパソコンユーザーにはノートを使っている人が結構いるみたいなので、 高速なビデオカードを持ってない人もいるわけです(実際に、Direct3DIMの機能をソフトウェアでエミュレート する、「HEL」というものを使うことができるのだが、これは遅くてしゃれになりません。 さらにいうならハードウェアによって動いたり、動かなかったりで、とても大変らしい)。 そういうことも考えると、こちらの方がいいかな〜と僕は考えています。んじゃ、作る!!
前置きはこのくらいにしてそろそろ作っていくことにします。座標変換を考えるために、アルゴリズムを考えておきましょう。
基本的には「この点を回転させたらどこへいくか」ということがわかればいいのです。 当たり前ですよね。ということは、変換後の座標=回転(変換前の座標) となります。回転には、高校2年生で習うはず(僕は高専生なのでちょっと違うかもしんないけど)の
y' = x・sinX + y・cosX
逆関数を求める
次変換関数がわかったところで、逆関数を求めてみましょう。先ほどの式を「移行」とかを使って、x,yについて解こうとすると(つまり、x=〜、y=〜の式にしようとすると)、 なんか連立方程式が出来そうで怖いですね。連立方程式なんてあまり解きたくありませんし、 解くのも難しそうです(おいおい、そんなんでいいのかよ・・・)。
というわけで、別の方法を考えてみます。唐突ですが次のような考え方は出来ないでしょうか?
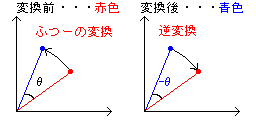
y = x'・sin-X + y'・cos-X
高速化 〜逆変換再び〜
前回、var x,y,u,v:Integer;
begin
for y:= 0 to 変形後の画像の高さ-1 do begin
for x:= 0 to 変形後の画像の幅-1 do begin
u=fx(x);
v=fy(y);
変形後の画像[x,y]:=変形前の画像[u,v];
end;
end;
end;
で画像変形ができるよー、でも遅くてゲームでは使い物にならないよー、といいました。
今回もその一例にあたります。だいたい、逆変換に三角関数が出てきている時点でアウトです。
じゃぁ、三角関数の値をあらかじめ計算しておいたテーブルを使ったらいいのか?しかし、
それには掛け算が必要になるので、遅そうです。じゃぁどうすればいいのかっちゅーと、
なんと、足し引き、シフトのみでいけるんですよ!!
クリッピング・・・何それ?
前回、「座標変換、落とし穴、高速化」の三つについてふれましたが、 画像変形においては「クリッピング」という処理が極めて重要になってきます。 これをきちんとやっておかないと、「アドレス違反」が起こり画像変形どころではありません。 下手すると「Windowsごと」落ちてしまいます。ホントです。 じゃぁ「クリッピング」とはいったい何物なのか?とりあえず外人ではなさそうです。 これは「変なところはいじくらないようにする処理」です(僕はそう思っている)。 たとえば、32×32のサイズの画像で「xが64、yが256の座標の色を教えて」といっても 「そんなんあるか、アホ!!」と怒られて(プログラムが落ちて)しまいます。 最悪のときは、横っ面をはたかれ(Windowsが落ち)ます。
完成 〜長いよ、これ〜
そうこうして出来あがったのが、下のソースです。クリッピングのせいでかなりややこしく、長くなっていますが、 やってることは簡単です。
ちなみにこのソースは、QuadrupleDコンポーネントがインストールされてないと、 使えません。さらにいうなら、16Bitカラー専用です。何かのたしになれば幸いです。
さらにいうと、高速化はあまりしていません。とりあえず固定小数点(?)を 使っていますが、アセンブラなどで最適化すれば、もっと速くなると思います。
それでは、がんばってください(^^;)
//回転後の矩形はうまくおさまっとるか?
function RotationClip(const Dest, Src: TDDDDGenSurface;
X, Y, Width, Height: Integer; cx, cy: Double; rotAngle: Integer;
var StartX, StartY, EndX, EndY: Integer): Boolean;
//回転後の座標を求める
function RotatePoint(ax, ay: Integer): TPoint;
var
c, s: Double;
begin
ax := Trunc(ax - Width *cx);
ay := Trunc(ay - Height*cy);
c := CosFast(rotAngle);
s := SinFast(rotAngle);
Result.X := X+Trunc(ax * c - ay * s);
Result.Y := Y+Trunc(ax * s + ay * c);
end;
var i: Integer;
Points: array[0..3] of TPoint;
begin
//四つの頂点を回転させる
Points[0] := RotatePoint(0, 0);
Points[1] := RotatePoint(Width, 0);
Points[2] := RotatePoint(0, Height);
Points[3] := RotatePoint(Width, Height);
//とりあえず左上っぽい座標wp設定しておく
StartX := Points[0].X;
StartY := Points[0].Y;
EndX := StartX;
EndY := StartY;
//左上、右下座標をセットする
for i:=1 to 3 do
with Points[i] do begin
StartX := Min(StartX, X); //一番小さいのが左
StartY := Min(StartY, Y); // 上
EndX := Max(EndX, X); //一番大きいのが右
EndY := Max(EndY, Y); // 下
end;
//サーフェースの大きさにあわせる
StartX := Max(StartX, 0);
StartY := Max(StartY, 0);
EndX := Min(EndX, Dest.Width);
EndY := Min(EndY, Dest.Height);
//範囲内にありますか
Result := (StartX<=Integer(Dest.Width )) and (EndX>0) and (EndX-StartX>0) and
(StartY<=Integer(Dest.Height)) and (EndY>0) and (EndY-StartY>0);
end;
procedure TRenderMachine.DrawRotate(src, dest: TDDDDGenSurface; x, y,
Width, Height: Integer; rec: TRect; cx, cy: Single; Transparent: Boolean;
rotAngle: Integer);
var
StartX, EndX, StartY, EndY: Integer; //最小内包矩形の頂点
dx,dy:Integer; //転送先へのアクセス用のカウンタ変数
sx,sy:Integer; //転送もとの座標
gx,gy,gsx,gsy:Integer;
c,s:Integer;
IncX,IncY:Integer;
ww,hh:Integer;
XScale,YScale:Single;
SrcRect:TRect;
SrcCol:WORD;
pDestLine,pDest,pSrcTop,pSrc:pWORD;
dddsd,sddsd:DDSurfaceDesc2;
begin
//クリッピング
if (Width = 0) or (Height = 0) then exit;
if Src.IsLost then exit;
if Dest.IsLost then exit;
if (Src = nil) or (Dest = nil) then exit;
if (rec.Left < 0) or
(rec.Top < 0) or
(rec.Right > Integer(Src.Width )) or
(rec.Bottom > Integer(Src.Height)) or
(rec.Left >= rec.Right ) or
(rec.Top >= rec.Bottom) then Exit;
rotAngle:=-rotAngle;
//回転後の点を求める
if not RotationClip(Dest, Src, X, Y, Width, Height, cx, cy, rotAngle,
StartX, StartY, EndX, EndY) then Exit;
XScale:=Width /GetRectWidth (Rec);
YScale:=Height/GetRectHeight(Rec);
//Sin,Cosの値を65536倍でゲット
c:=Round(CosFast(-rotAngle)*65536/XScale);
s:=Round(SinFast(-rotAngle)*65536/YScale);
IncX:= Round(CosFast(rotAngle)*65536/XScale);
IncY:=-Round(SinFast(rotAngle)*65536/YScale);
//回転後の左上座標を-rotAngle回転させて、変換前の座標を求める(逆変換)
gsx:=(StartX-X)*c+(Y-StartY)*s+Round(GetRectWidth (rec)*cx*65536);
gsy:=(StartX-X)*s-(Y-StartY)*c+Round(GetRectHeight(rec)*cy*65536);
//ロック
Dest.Lock(dddsd);
Src.Lock(sddsd);
//転送先のポインタを左上にセット
pDestLine:=dddsd.lpSurface;
Inc(pDestLine,StartX+StartY*Dest.Width);
//転送元のポインタを左上にセット
pSrcTop:=sddsd.lpSurface;
Inc(pSrcTop,Rec.Left+Rec.Top*Src.Width);
SrcRect:=Rect(0,0,GetRectWidth(Rec),GetRectHeight(Rec));
//最小内包矩形の全ピクセルにアクセス
for dy:= StartY to EndY-1 do begin
pDest:=pDestLine;
gx:=gsx;
gy:=gsy;
for dx:= StartX to EndX-1 do begin
//座標を進める
Inc(gx,IncX);
Inc(gy,IncY);
//固定小数点をもとにもどす
sx:=gx shr 16; sy:=gy shr 16;
//アドレス的には大丈夫?
if (sx >= SrcRect.Left)and(sx < SrcRect.Right)and(sy >= SrcRect.Top)and(sy < SrcRect.Bottom) then begin
pSrc:=pSrcTop;
Inc(pSrc,sx+sy*Src.Width);
SrcCol:=pSrc^;
if SrcCol <> Src.ColorKey then pDest^:=SrcCol;
end;
Inc(pDest); //転送先のポインタを右へ進める
end;
Inc(pDestLine,Dest.Width); //転送先のポインタを次のラインの左端に
Dec(gsx,IncY);
Inc(gsy,IncX);
end;
//アンロック
Dest.UnLock;
Src.UnLock;
end;
それでは、お待ちかねのサンプルです。拡大・縮小についてはまだ実装していません。
rotate.zip 189KB
なーんて、たいそうなことをいっておりますが、結局のところ僕が使いたいだけです。 今回のやつだと、 「DelphiXからQuadruple Dにいったはいいけど、画像回転関数がなーーーい!!」 ってのが理由です(^^;)画像回転はポピュラーな割に、PASCALの簡単なコードが手元にないということ、 日本語のページでは回転してるのをあまり見たこと無いこと、そしてWinGLへの ほのかな対抗意識があったので、自分で作るしかありませんでした (うまくいってなかったときは「WinGL」にレジストするか?・・・」とかも思いましたが)。
※QuadrupleD
DELPHIでDirectXが使える有名なコンポーネント。
サンプル・チュートリアルの豊富さが魅力。
※DelphiX
DELPHIでDirectXが使える有名なコンポーネント。
画像合成関数が非常に豊富。
※三角関数
高校生になるとみんなを苦しめる、数学のやつ。
公式がいっぱいあるが、原理がわかれば全部導けます(覚えたほうが速いけど)。
※テーブル
高速化のためによく使われるテクニックで、よく使う計算をあらかじめ
計算しておいてそれを配列に格納しておき、使いたいときに引き出すというもの。
覚えておくと、世界が広がります。
※シフト
2,4,6,8,16・・・・という2の乗数にあたる数値の掛け算を、高速に出来る。
実際には、値を左右に何ビットかずらして(シフトさせて)いるだけ。
知っておきたい、この一品。