(1) N ������ ��(����2) �Ŋ�����Ƃ� (�Q�̐����̐ςɕ���)
�@N�^�� ������������C(A-1) ���� k , n �ɂ��āC
�@�@�@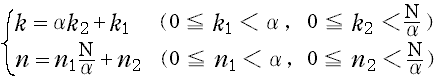
�Ƃ����āC���̂Ƃ� (A-1) ���͎��̂悤�ɕό`�ł���B
�@�@�@ 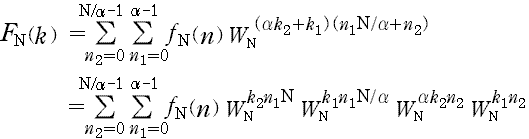
������ (B-1a, b) ���g���ƁC
�@�@�@�@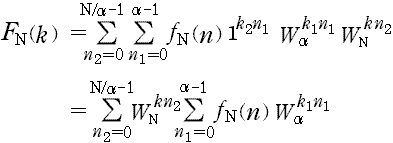 �@�c�c�c(C-1)
�@�c�c�c(C-1)
�@(A-1) �ł́CW �̌v�Z�������ƁCN2 ����x�̕��f���̊|���Z������̂ɑ��C(C-1) �ł́C
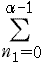 �@�̂Ƃ���� ��N ����x,
�@�̂Ƃ���� ��N ����x,
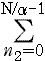 �@�̂Ƃ���� N2�^�� ����x,
�@�̂Ƃ���� N2�^�� ����x,
�Ȃ̂ŁC�ʏ�́C�|���Z�̉����Ȃ茸�邱�ƂɂȂ�B���������āC�� ������Ɂw�����x���Ă����C�|���Z�̉��ǂ�ǂ��Ă����Ǝv����B
 TOP�y�[�W
TOP�y�[�W