（← 前のページへ　//　次のページへ →）

３. N ＝α1α2 ……αs ,(α1,α2,……,αs≧2) のときの漸化式＜(1),(2)＞ 　まず，次のような変数を導入する。 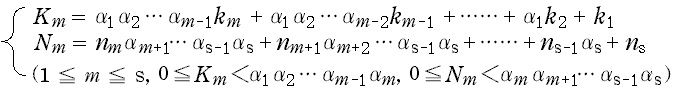　特に，K1 ＝ k1， Ks ＝ k ，N1 ＝ n ，Ns ＝ ns　である。 これらを使って，(C-a, b) 式から以下のような漸化式を作ってみる。 (1) nmについてまとめたとき …… (C-a) より 　このとき (C-a) 式は，次のように書き直すことができる。 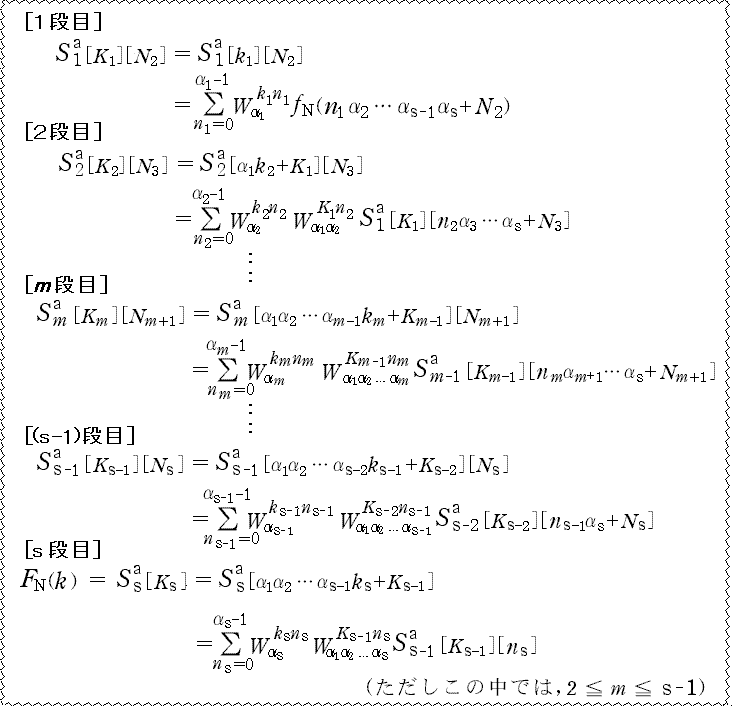………(D-1) 　なお，この場合は，『時間間引きの FFT』と呼ばれる。 (2) kmについてまとめたとき …… (C-b) より 　このとき (C-b) 式は，次のように書き直すことができる。 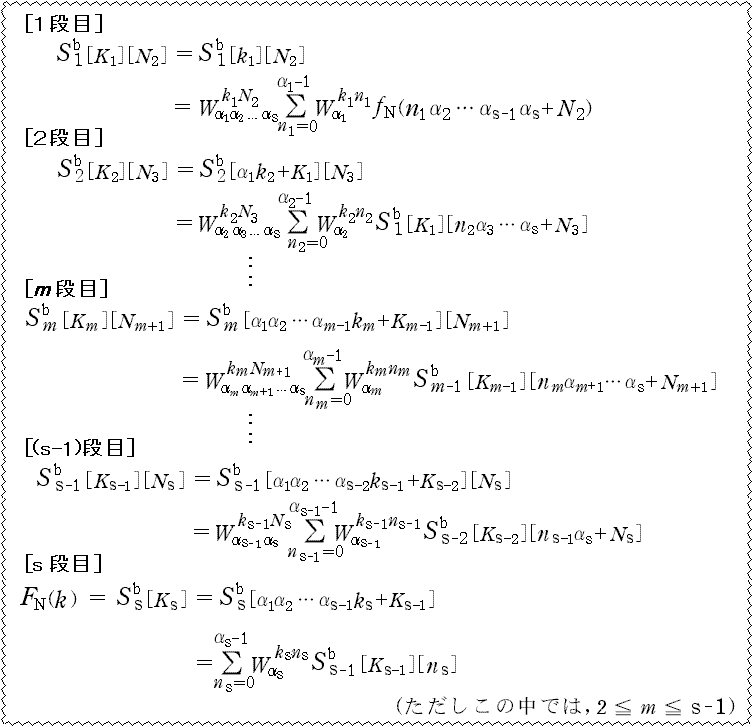………(D-2) 　なお，この場合は，『周波数間引きの FFT』と呼ばれる。 　ここで (D-1, 2) の [m 段目] に注目してみる。この段階で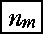， Sm -1[Km -1][Nm] ： 変数 (km -1 ,……, k2 , k1 , , nm +1 ,……, ns -1 , ns ) から Sm[Km][Nm +1] ： 変数 ( 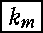, km -1,……, k2, k1, nm +1 ,……, ns -1 , ns ) になっていることを注意しておこう。（S の上の添え字 a, b は省略）

（← 前のページへ　//　次のページへ →）