4. (D-1, 2) の漸化式と計算中のデータとの対応
ここで念のため,次のことを繰り返しておく。
DFTの式
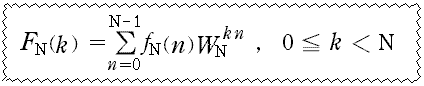 ………(A-1) ………(A-1)
の計算は,N =α1α2…αs (α1 , α2 ,……,αs≧2) のとき,(D-1, 2) のように 『 s 段』 の計算で実行できる。ただし,
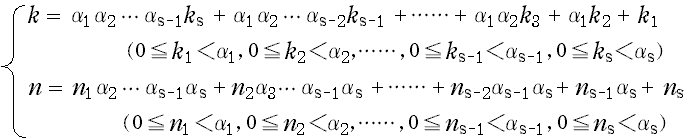
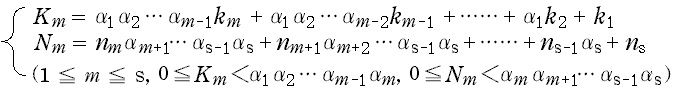
特に,K1 = k1, Ks = k ,N1 = n ,Ns = ns である。
このとき,
k の変数 (ks, ks -1,……, k2, k1) で,ksが『最上位』,k1が『最下位』
n の変数 (n1, n2,……, ns -1, ns ) で,n1が『最上位』,nsが『最下位』
であることに注意しよう。
ここで (D-1, 2) の [m 段目] では (S の上の添え字 a, b は省略)
Sm -1[Km -1][Nm] : Km -1(km -1,……, k2, k1 ) ,Nm( 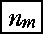 , nm +1,……, ns -1, ns ) , nm +1,……, ns -1, ns )
から
Sm [Km][Nm +1] : Km( 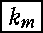 , km -1,……, k2, k1 ),Nm +1( nm +1,……, ns -1, ns ) , km -1,……, k2, k1 ),Nm +1( nm +1,……, ns -1, ns )
になっていることにも注意しておこう。
以上のことを踏まえて,実際にコンピュータプログラムを作成する上で,このような変数 (kmやnmなど) をどう捕らえるかを考えてみる。
(1) k , n 内の変数の『上下関係』を変えない(『メモリ』を多めに使う)
Smの『添え字変数』k 'm を次のようにおく。
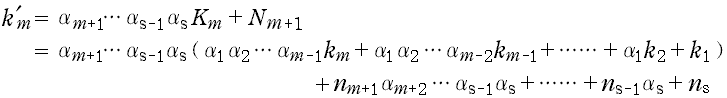
………(E-1)
このとき k 'm の変数
(km , km -1,……, k2, k1, nm +1,……, ns -1, ns )
において,km が『最上位』,nsが『最下位』である。
このとき,(D-1, 2) の計算では,『添え字変数』k 'm は次のように変化する。
- n : (
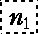 , n2, n3,……, ns -1, ns ) , n2, n3,……, ns -1, ns )
- [1段目] → ↓
- k '1: (
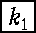 , , 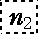 , n3,……, ns -1, ns ) , n3,……, ns -1, ns )
- [2段目] → ↓
- k '2: (
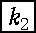 , k1, , k1, 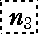 ,……, ns -1, ns ) ,……, ns -1, ns )
- ↓
- :
- :
- ↓
- k 'm -1: (
 ,……, k2, k1, ,……, k2, k1, 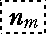 , nm +1,……, ns -1, ns ) , nm +1,……, ns -1, ns )
- [m 段目] →↓
- k 'm: (
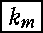 , km -1,……, k2, k1, , km -1,……, k2, k1, 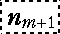 ,……, ns -1, ns ) ,……, ns -1, ns )
- ↓
- :
- :
- ↓
- k 's-1: (
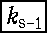 , ……, k2, k1, , ……, k2, k1, 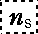 ) )
- [ s 段目] →↓
- k 's: (
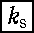 , ……, k2, k1 ) , ……, k2, k1 )
このとき k 'm -1 と k 'm では,『位』が同じ共通の変数は,nm +1,……, ns -1, ns だけなので,『小さい作業領域』での,Sm -1の『データ領域』へのSm のデータの上書きはできない。したがって,『計算途中用のデータ配列領域』が余分に必要である。
なお,最終的に k 's= k となるので,データを並べ替える必要はない。
更に『Wの値の表』( (D-1)では 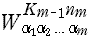 ,(D-2)では ,(D-2)では 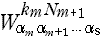 )の並べ替えも必要ない。 )の並べ替えも必要ない。
(2) 『計算途中用のデータ配列領域』を使わない
i ) 計算後に並べ替える
まず,Km 内の変数の『上下関係』を逆にしたものを
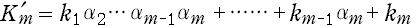
とおき,Smの『添え字変数』k 'm を次のようにとる。
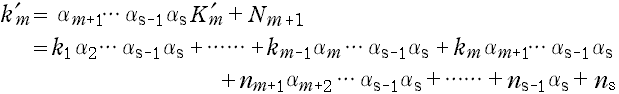
………(E-2i)
このとき k 'm の変数
(k1, k2,……, km -1, km , nm +1,……, ns -1, ns )
において,k1が『最上位』,nsが『最下位』である。
こうすると,(D-1, 2) の計算では,『添え字変数』k 'm は次のように変化する。
n : ( 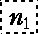 , n2, n3,……, ns -1, ns ) , n2, n3,……, ns -1, ns )
- [1段目] → ↓
- k '1: (
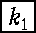 , , 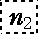 , n3,……, ns -1, ns ) , n3,……, ns -1, ns )
- [2段目] → ↓
- k '2: ( k1,
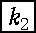 , , 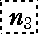 ,……, ns -1, ns ) ,……, ns -1, ns )
- ↓
- :
- :
- ↓
- k 'm -1: (k1, k2,……,
 , , 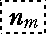 , nm +1,……, ns -1, ns ) , nm +1,……, ns -1, ns )
- [m 段目] →↓
- k 'm: (k1, k2,……, km -1,
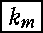 , , 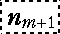 ,……, ns -1, ns ) ,……, ns -1, ns )
- ↓
- :
- :
- ↓
- k 's-1: (k1, k2,……,
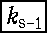 , , 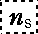 ) )
- [ s 段目] →↓
- k 's: (k1, k2,……, ks -1,
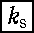 ) )
このとき k 'm -1 と k 'm では,『位』が同じ共通の変数は,km と nm 以外すべてなので,『小さい作業領域』での,Sm -1の『データ領域』へのSm のデータの上書きができる。したがって,余分の『計算途中用のデータ配列領域』は必要ない。
しかし,最終的には k 's= k とはならず,
k の変数 (ks, ks -1,……, k2, k1) は,ksが『最上位』,k1が『最下位』
k 'sの変数 (k1, k2,……, ks -1, ks) は,k1が『最上位』,ksが『最下位』
なので, 計算後にデータの並べ替えが必要となる。
a) (D-1) 式では
[m 段目] の 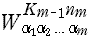 の Km -1では, の Km -1では,
km -1 が『最上位』,k1が『最下位』
であるのに対し,(E-2i) 式の K 'mでは,
k1が『最上位』,km が『最下位』
になっている。このことから,『Wの値の表』を使うときには,計算時に『表の並べ替え』をする必要があるのがわかる。
b) (D-2) 式では
[m 段目] の 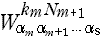 の Nm +1が,そのまま (E-2i) 式の k 'm に含まれている。したがって,『Wの値の表』を並べ替える必要はない。 の Nm +1が,そのまま (E-2i) 式の k 'm に含まれている。したがって,『Wの値の表』を並べ替える必要はない。
ii ) 計算前に並べ替える
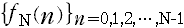 から から 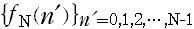 に並べ替えたとする。 に並べ替えたとする。
ただし,
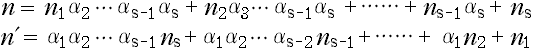
である。ここで,Nm 内の変数の『上下関係』を逆にしたものを
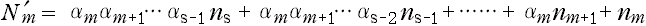
とすると,Smの『添え字変数』k 'm は次のようにおける。
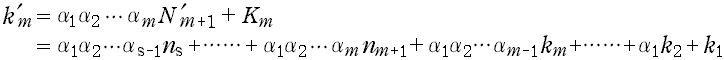
………(E-2ii)
なお,k 'm の変数
(ns, ns -1,……, nm +1, km ,……, k2, k1)
において,ns が『最上位』,k1が『最下位』である。
このとき,(D-1, 2) の計算では,『添え字変数』k 'm は次のように変化する。
- n ' : ( ns, ns -1,……, n3, n2,
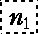 ) )
- [1段目] → ↓
- k '1: ( ns, ns -1,……, n3,
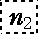 , , 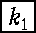 ) )
- [2段目] → ↓
- k '2: ( ns, ns -1,……,
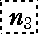 , , 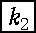 , k1) , k1)
- ↓
- :
- :
- ↓
- k 'm -1: ( ns, ns -1,……, nm +1,
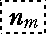 , ,  ,……, k2, k1) ,……, k2, k1)
- [m 段目] →↓
- k 'm: ( ns, ns -1,……,
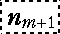 , , 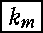 , km -1, ……, k2, k1) , km -1, ……, k2, k1)
- ↓
- :
- :
- ↓
- k 's-1: (
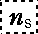 , , 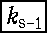 , ……, k2, k1) , ……, k2, k1)
- [ s 段目] →↓
- k 's: (
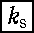 , ……, k2, k1 ) , ……, k2, k1 )
このとき k 'm -1 と k 'm では,『位』が同じ共通の変数は,km と nm 以外すべてなので,『小さい作業領域』での,Sm -1の『データ領域』へのSm のデータの上書きができる。したがって,余分な『計算途中用のデータ配列領域』は必要ない。
なお,最終的に k 's= k となっているので,計算後にデータの並べ替える必要はない。
a) (D-1) 式では
[m 段目] の 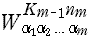 の Km -1 が,そのまま (E-2ii) 式の k 'm に含まれている。したがって『Wの値の表』を並べ替える必要はない。 の Km -1 が,そのまま (E-2ii) 式の k 'm に含まれている。したがって『Wの値の表』を並べ替える必要はない。
b) (D-2) 式では
[m 段目] の 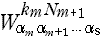 の Nm +1では, の Nm +1では,
nm +1 が『最上位』, ns が『最下位』
であるのに対し,(E-2ii) 式の N 'm +1では,
ns が『最上位』,nm +1 が『最下位』
になっている。このことから,『Wの値の表』を使うときには,計算時に『表の並べ替え』をする必要があるのがわかる。
|
 TOPページ
TOPページ