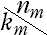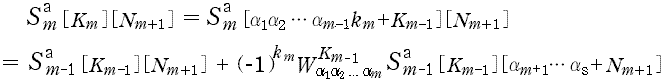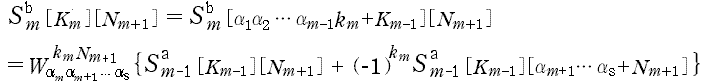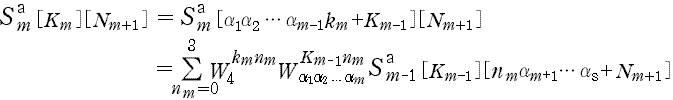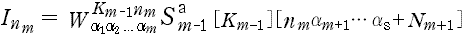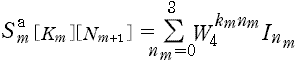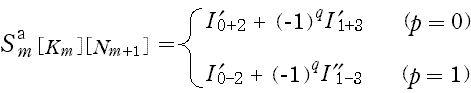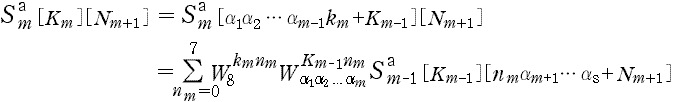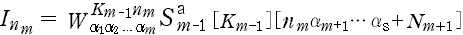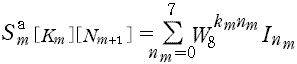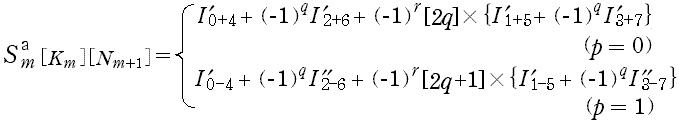3. N =α1α2 ……αs ,(α1,α2,……,αs≧2) のときの漸化式<(3)>
(3) αm= 2, 4, 8 (21, 22, 23) のときの 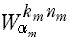
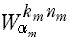 (αm= 2, 4, 8) の値を,次のように,複素平面上の単位円に示してみた。 (αm= 2, 4, 8) の値を,次のように,複素平面上の単位円に示してみた。
![[0]〜[7]の値](03_06.gif) 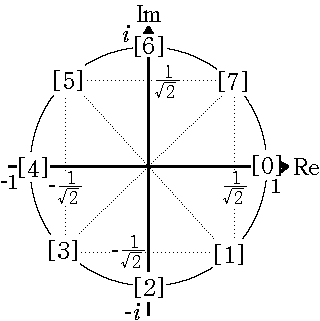
なお,kmnm≧αm のときについては,
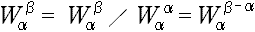
が成り立つことから,( kmnm÷αm ) の余りで考えれば良い。
また,[0] 〜 [7] を複素数 z =a −i b に掛けたときの効果は次の通りである。
[0]×z = z (そのまま)
[1]×z = {(a −b)−i (a+b)}/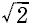
[2]×z = - b −i a
[3]×z = {- (a+b)−i (a - b)}/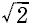 = [1]×[2]×z = [1]×[2]×z
[4]×z = - [0]×z
[5]×z = - [1]×z
[6]×z = - [2]×z
[7]×z = - [3]×z
以上のことを次のように表にまとめた。
i ) αm= 2 のとき
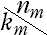
|
0
|
1
|
|
0
|
[0]
|
[0]
|
|
1
|
[0]
|
- [0]
| 0≦km<2,0≦nm<2 であることから,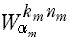 を掛ける効果は右表のようになる。 を掛ける効果は右表のようになる。
このように,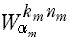 を掛けても,複素数の掛け算の回数は増えない。 を掛けても,複素数の掛け算の回数は増えない。
なお (D-1, 2) の [m 段目] は,それぞれ次のようになる。
- a) (D-1) 式では,
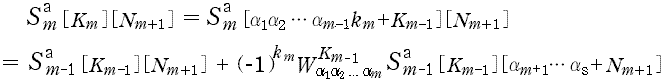
- b) (D-2) 式では,
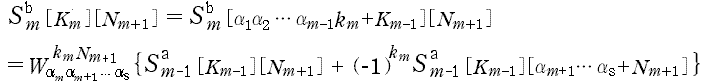
このとき,この段での複素数の掛け算の回数は,
(Km -1)max×(Nm +1)max×1 ≒ N/2 程度
であるのがわかる。
特に,α1=α2=……=αs= 2 のときのすべての段での合計回数は,
(s - 1)×N/2 = (log2N - 1)・N/2 程度
である。( a)では m =1,b)では m =s のとき複素数の掛け算がない。)
ii ) αm= 4 のとき
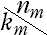
|
0
|
1
|
2
|
3
|
|
0
|
[0]
|
[0]
|
[0]
|
[0]
|
|
1
|
[0]
|
[2]
|
- [0]
|
- [2]
|
|
2
|
[0]
|
- [0]
|
[0]
|
- [0]
|
|
3
|
[0]
|
- [2]
|
- [0]
|
[2]
| 0≦km<4,0≦nm<4 であることから,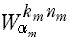 を掛ける効果は右表のようになる。 を掛ける効果は右表のようになる。
このように,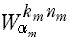 を掛けても,実部と虚部の入れ替えはあるが,複素数の掛け算の回数は増えない。 を掛けても,実部と虚部の入れ替えはあるが,複素数の掛け算の回数は増えない。
なお (D-1, 2) の [m 段目] は,それぞれ次のようになる。
- a) (D-1) 式では,
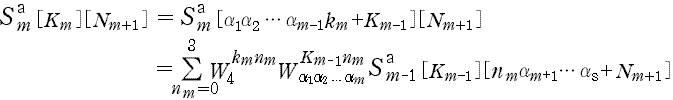
- である。
- ここで,
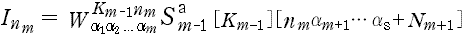
- とおいてしまうと,I nmの値は km のすべての値(km= 0, 1, 2, 3) で『共通』であり,また
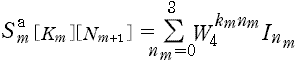
- となる。ここで,
- I '0±2 = I 0±I 2 ,I '1±3= I 1±I 3 ,I ''1-3= [2]×I '1-3
- km= 2q +p (0≦p <2,0≦q <2)
- とおくと次のようになる。
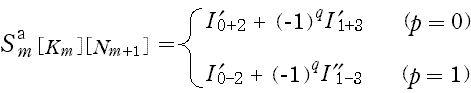
- b) (D-2 )式でも,a) とほぼ同様である。
このとき,この段での複素数の掛け算の回数は,
(Km -1)max×(Nm +1)max×3 ≒ 3N/4 程度
である。
特に,α1=α2=……=αs= 4 のときのすべての段での合計回数は,
(log4N - 1)×3N/4 = (log2N - 2)・3N/8 程度
である。( a)では m =1,b)では m =s のとき複素数の掛け算がない。)
iii ) αm= 8 のとき
0≦km<8,0≦km<8であることから,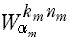 を掛ける効果は次の表のようになる。 を掛ける効果は次の表のようになる。
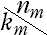
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
0
|
[0]
|
[0]
|
[0]
|
[0]
|
[0]
|
[0]
|
[0]
|
[0]
|
|
1
|
[0]
|
[1]
|
[2]
|
[3]
|
- [0]
|
- [1]
|
- [2]
|
- [3]
|
|
2
|
[0]
|
[2]
|
- [0]
|
- [2]
|
[0]
|
[2]
|
- [0]
|
- [2]
|
|
3
|
[0]
|
[3]
|
- [2]
|
[1]
|
- [0]
|
- [3]
|
[2]
|
- [1]
|
|
4
|
[0]
|
- [0]
|
[0]
|
- [0]
|
[0]
|
- [0]
|
[0]
|
- [0]
|
|
5
|
[0]
|
- [1]
|
[2]
|
- [3]
|
- [0]
|
[1]
|
- [2]
|
[3]
|
|
6
|
[0]
|
- [2]
|
- [0]
|
[2]
|
[0]
|
- [2]
|
- [0]
|
[2]
|
|
7
|
[0]
|
- [3]
|
- [2]
|
- [1]
|
- [0]
|
[3]
|
[2]
|
[1]
|
なお (D-1, 2) の [m 段目] は,次のようになる。
- a) (D-1) 式では,
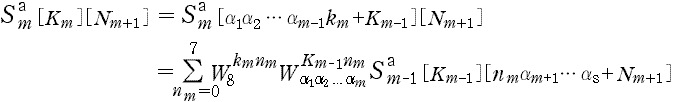
- である。
- ここで,
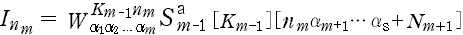
- とおいてしまうと,I nmの値は km のすべての値(km= 0 〜 7) で『共通』であり,
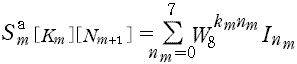
- となる。ここで,
- I '0±4 = I 0±I 4 ,I '2±6= I 2±I 6 ,I ''2-6= [2]×I '2-6
- I '1±5 = I 1±I 5 ,I '3±7= I 3±I 7 ,I ''3-7= [2]×I '3-7
- km= 4r + 2q +p (0≦p <2,0≦q <2,0≦r <2)
- とおき,
- [3]×z = [1]×[2]×z
- [1]×z = - (- [1]×z ) = - [5]×z = - [3]×[2]×z
- に注意すると,
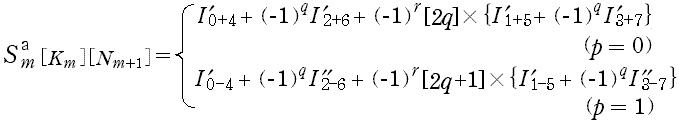
- となる。
- また [1]×,[3]× はそれぞれ,複素数の掛け算 1/2 回に相当するので,
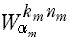 を掛けることにより複素数の掛け算が1回分増えている。 を掛けることにより複素数の掛け算が1回分増えている。
- b) (D-2 )式でも,a) とほぼ同様である。
なお,この段での複素数の掛け算の回数は,
(Km -1)max×(Nm +1)max×(7 + 1) ≒ N 程度
である。
特に,α1=α2=……=αs= 8 のときのすべての段での合計回数は,
(log8N - 1)・N + N/8 = (N/3)・log2N - 7N/8 程度
である。( a) では m =1,b) では m = s のとき複素数の掛け算は,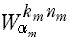 のみ。) のみ。)
以上 i ),ii ),iii ) からわかるように,αm= 2 のみで計算するよりも,4 , 8 も適切に使う方が,より速く計算できることが予想できる。
また,αm= 16 , 32 , … の方がより掛け算回数が減ると考えられるが,場合分けが複雑になったり加減算が増えたりして,かえって『効率』が悪くなるかもしれない。[→ A. 参考文献など (2)]
|
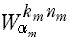
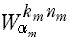 (αm= 2, 4, 8) の値を,次のように,複素平面上の単位円に示してみた。
(αm= 2, 4, 8) の値を,次のように,複素平面上の単位円に示してみた。![[0]〜[7]の値](03_06.gif)

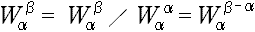
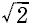
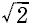 = [1]×[2]×z
= [1]×[2]×z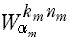 を掛ける効果は右表のようになる。
を掛ける効果は右表のようになる。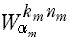 を掛けても,複素数の掛け算の回数は増えない。
を掛けても,複素数の掛け算の回数は増えない。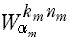 を掛ける効果は右表のようになる。
を掛ける効果は右表のようになる。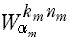 を掛けても,実部と虚部の入れ替えはあるが,複素数の掛け算の回数は増えない。
を掛けても,実部と虚部の入れ替えはあるが,複素数の掛け算の回数は増えない。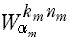 を掛ける効果は次の表のようになる。
を掛ける効果は次の表のようになる。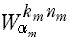 のみ。)
のみ。)