そういうわけで、今日は「坂道とのあたり判定」をレッツシンキング。 坂道テクは、スーパーファミコンくらいのころから、頻繁に使われるようになったと思います（マリオとか）。 スーファミ時代から使われているテクを、高速なCPUを持つパソコンで実現できないはずがない！！ということで（もちろん、頭が働けばの話だけど・・・）。 実際、パソコンのゲームでそういうのは見たことがないですしね。そういうわけで、イメージから入ってみます。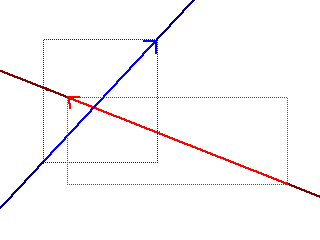

えーと、青と赤、点線で囲まれたふたつの線分がありますね。直線ではなく線分として考えてください。理由は後ほど。 さて、このふたつの明らかに交わっていますね。それでは、ちょっと数学っぽくいってみます。

y=a1x+b1,y=a2x+b1であらわされる直線が二つある。
この二直線が交わる条件を示せ（ただし、ここでは線分ではなく直線である）。

中学生のころによくみたような問題ですね。では、これを解いてみてください。 ・・・解けましたか？一応、僕が解いたものを挙げてみます。

y=a1x+b1・・・(1) y=a2x+b2・・・(2) この二直線が交わるとすると
a1x+b1=a2x+b2・・・(3)
(a1-a2)x=b2-b1
x=(b2-b1)/(a1-a2)・・・(4)

(3)に(4)に代入する

a1(b2-b1)/(a1-a2)+b1=a2(b2-b1)/(a1-a2)+b2

この式が成り立てば、二直線は交わる（終わり）

こんなふうになるのかな？間違ってたら、ご指摘をお願いします。しかし、これはあくまでも数学的に解いただけなので、 コンピュータ上でもこれと同じようになるとは限りません。計算には必ず「誤差」がのりますからね。 といっても、しょうがないのでひとまずここでは「誤差なし」として考えていきます。たまにはそんなことも必要です（ほんとか？）。

さて、直線の交わりさえ検出できればあとは簡単ですね。上の図の「点線」同士が重なっていれば、二線分は交わったことになりますよね。 つまり、直線の交わりさえ検出できれば、後はその線分の範囲のあたり判定となります。矩形同士、円同士、矩形と円・・・など 好きなように出来ます。

ここまで来れば、坂道とのあたり判定は簡単（？）なはずです。ひとまず「概念」として全部見てきたので、 多少問題はあると思いますが・・・。ちなみに、坂道の角度を45度に制限とかそういう条件を加えてやれば、 もっと簡単に判定できると思います。恐らくスーファミの坂道判定などは、そのような「だまし」テクニックの 方が多いんじゃないのかな？。

というわけで、次はいろいろあたり判定を見ていきたいと思います。