坂道の表現法といっても、「描画」に関するものではありません。
実世界で言うなら「人間が坂道に沿って歩く」アルゴリズム、ってなところでしょうか。
実世界で当たり前におきていることって結構面倒なものが多い、と再度実感する瞬間でもあります。

僕の知るところによると、新しいものでは海外のQuake系統の3Dゲーム、
古いところではファミコンの「スーパーマリオ3」以降や「くにおくん」シリーズと、
かなり昔から使われているテクニックでもあります。ファミコンの詳しいスペックは
知りませんが、このころからできるってことは、かなり簡単な処理、ってことが予想されますね。


私がアドバイスしてもらった処理では「三角関数」をちょこっと使うだけです。
(実は「直線」の式を使って同じことができるし)
「三角関数」といっても恐れるほどのものではありません。加法定理など、テストで学生を
さんざん苦しめたような難しいものは一切いりません。
まさに、「基礎」だけわかってればいいのです。三角関数の説明については こちらをどうぞ。
説明が分かりにくかったらサーチエンジンで探してください(^^;)

文章では説明しにくいので、いきなり図。

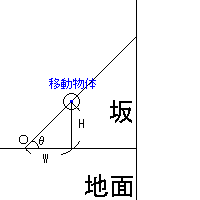
坂道の角度を「θ」とします。この図では「θ」は「45°」とします。
「Ｏ」は原点です。
「移動物体」の真ん中にある「青い店」はもちろん物体の中心点です。
ここが判定の基準となります。
「移動物体」と「Ｏ」との距離を「Ｗ」、高さを「Ｈ」とします。

上の図では、「移動物体」の位置がわかっていますが、実際にはどうやって求めたかっていうと、
「移動物体」が横に「W」だけ移動したとして、そのときの高さを求める、となります。
さて、ここで三角関数の登場となります。三角関数を知っている方は図と見た時点でおわかりになった
ことだろうと思います。それでは、式にしてみます。

H = W * Sin(θ)

となりますね。というか、なるんですよ(^^;)
それでは、三角関数を知らない人のための説明に移ります。

上の図をグラフとすると、なんとなくみえてくるとおもうのですが、
坂道の傾きを、「直線の式」であらわせばいいのです。簡単ですね。
ということで、傾きをaとしてまたもや式を立ててみます。
H = a * W
となると思います。こっちの方が簡単かも(^^;)
どちらを使うかはみなさん次第、ということで。


さて、上記のものは「一次方程式」、つまり「片方分かればもうひとつの分かる」という
やつであることに気づいてくれたでしょうか？
つまり、単純な坂道だけにかかわらず「一次方程式」で表現できるものであれば、
どんなものでも表現できるということですね。
「丸っこい坂」なども「円の方程式」、「波のような坂」なら「三角関数」を使えばいい、
というだけです。

あとは、みなさんのアイデア次第ということで。
何か面白いものがあれば教えてくださいね。

疑問、質問があればこちらまで。