− 科学的思考(2) −
フラクタル的人生考
1998.09.27 swing
22.08.31.update
素数階段
|
 |
 |
 |
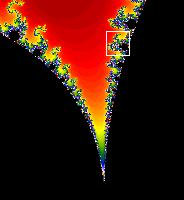
(a)集合の全体図
|
(b)図(a)の白線四角部分
|
(c)図(b)の白線四角部分
|
 |
 |
 |
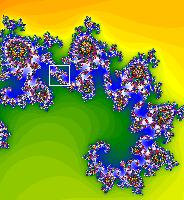
| (d)図(c)の白線四角部分 |
(e)図(d)の白線四角部分 |
(f)図(e)の白線四角部分 |
|
図1.「フラク太郎」で描いたマンデルブロー集合の全体と部分
【 はじめに 】
・私は1990年頃に「フラクタル」に出会い、大変大きな衝撃を受けたました。
そして、このフラクタルに魅了され、物の見方・考え方に少なからぬ影響を受けました。
・私が影響を受けた点は、フラクタルの最大の特徴である「自己相似性」と言う概念です
ので、このページではその「自己相似性」についてと、その考え方の応用について書い
てみようと思います。
・このページのタイトルを「フラクタル的人生考」としましたが、人生を語るには私は未だ若過ぎ
ますし、知らないことが多過ぎるとは思いますが、私にとってはまさに「物の見方についての基
本的な考え方」が含まれているものですから、恥ずかしながら敢えてこのようなタイトルにした
次第です。
・フラクタル(=FRACTAL)と言ってもご存知ない方の方が多いことでしょう。
・フラクタルとは、正確には「フラクタル幾何学」と言う数学のことを指します。その内容は工学
や生物学にも応用され、「非線型」と言われる高度な分野の解析手段として「カオス理論」など
と共に利用されている、比較的新しい理論です。
・自然の造形の美しさの中などにも、このフラクタルが含まれていると言われています。
→本来のフラクタル図形は、横軸に実数、縦軸に虚数(=i)を配した
「複素平面」上で計算して描画するものですが、このページでは複素数については触れず、
自己相似性についてのみ考えることにしました。
→フラクタル図形の驚異は、上図「マンデルブロー集合」などもそうですが、極単純な複素数
の式についての計算なんですが、その式を何千回何万回と繰り返し計算(ネスティング)す
ることにより、予想を越えた複雑で奇妙な図形を生み出すことができる点にあります。
そして、もし計算機を用いずに、手計算でこの図形を描く計算をしたら、きっと 100年以上
かかってしまうことでしょう!
・フラクタル理論は、1975年フランスのマンデルブロー以来電子計算機の高速化とともに、発展し
て来ました。
・フラクタル図形の描画は単純計算とは言え、膨大な回数の繰り返しをしなければならないため、
当初はIBMの大型電子計算機でしかできなかったのですが、技術の進歩はありがたいものです!
..今では、自宅のパソコンでも描画して楽しむことができるようになりました!
..つまり、計算速度と言う「量の変化」がフラクタル幾何学の誕生と言う「質の変化」を生み出
したんです!
→「計算に100年以上かかる」ものは、「不可能だね」と言い、
「計算が10分以内でできる」ものは「簡単だあ」と言います!
→遺伝子の分析を行う「ヒトゲノム計画」なんかでも高速な計算機なしでは、到底考えられな
いものでしょう。
・参考図書とフラクタル描画ソフトのダウンロードについてご案内します。
(今も市販されているかどうかは調べてません)
<参考図書>
1.『カオスとフラクタル』 …入門書
山口 昌哉 著、講談社(BLUE BACKS-B652)
2.『フラクタルって何だろう』…入門書
高安 秀樹、高安 美佐子 著、ダイヤモンド社(830045)
3.『フラクタル』 …専門書
高安 秀樹 著、朝倉書店
4.『フラクタルの美』 …カラー写真集(10年前で \4,800!)
宇敷 重広 訳、シュプリンガーフェアラーク東京
<ソフトウェアのダウンロード>
・『フラク太郎』は、こちらでダウンロードできますが、私が持っているソフト
のバージョンは 3.3b ですが、現在配布されているものは 1.0 です。
当時の作者のサイトがなくなってしまったため、経緯はわかりません。
【 1.フラクタル図形の自己相似性 】
1-1.一次元のフラクタル図形
・「自己相似性」とは、「全体と、その部分が相似している」と言うことなんですが、
それだけじゃ分りにくいでしょうから、次の「図2.」で説明します。
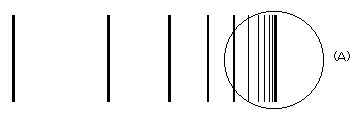 図2.一次元のフラクタル図形
・この図には、縦線が何本か引いてありますが、左から右に行くに従って、その間隔が
一定の比率で狭まっています。(この図では約0.7倍)
・幅がどんどん狭まって行くと「円(A)」の中心部分あたりで、それ以上右には行けな
くなる限界に行き着きます。
・この「円(A)」の部分を虫めがねで覗いて見ましょう..どんな図が見えるでしょうか?
...
・図形全体と同様の線の並びが見えるでしょう!?
...
・では、思いきって倍率を上げて、電子顕微鏡で10万倍にして覗いて見ましょう!..
今度は何が見えると思いますか?
...
・答えは同じです..つまり、図2の図形は、どの部分をどう拡大しても、見える図形は、
全体の図形と同じ形をしているのです!
<線路の比喩>
・このような経験をしたことはないでしょうか..子供のころ、電車の一番前に乗って、
ずっと先まで伸びている線路を見ていた、なんて..
・その時見えた線路は先に行くほど幅が狭くなって見え、そのずっと先では「ほとんど
一点」にくっ付いているように見えます。
→その時、枕木は「図2」のように、先に行くほど、幅がだんだんと狭まって見え
ますよね。
…線路は、本当にくっ付いているんだろうか…
…あそこまで行ったら、どうなってるんだろう…
・1時間ほどその電車に乗っていたとしましょう..
前に「ほとんど一点」に見えていた所あたりまで、もう来たはずなんだけど、線路の
見え方には何の変化も見えない..
…やっとここまで来たのに…
…さっき(1時間前に)見えていた線路の景色と同じだ!?…
…今いる場所は確かに違うはずなのに、見える景色は同じだ!
…どうしてなんだろう?
1-2.フラクタルの樹
・下の図3〜5は「フラクタルの樹」です。この図の場合は、幹から枝を2本だし、そ
の枝が また二つに枝分かれしています。
→ 1本が2本 → 2本が4本 → 4本が8本 → 8本が16本
→ 16本が32本 → 32本が64本 → 64本が128本 → (ふうぅ..!)
・この図を描くために、初めてwindowsの「ペイント」を使いました。
・枝分かれする時、枝の長さは一定の比率で短くなり、枝の角度は一定であるものとし
て書かれています。(この図では約0.7倍)
図2.一次元のフラクタル図形
・この図には、縦線が何本か引いてありますが、左から右に行くに従って、その間隔が
一定の比率で狭まっています。(この図では約0.7倍)
・幅がどんどん狭まって行くと「円(A)」の中心部分あたりで、それ以上右には行けな
くなる限界に行き着きます。
・この「円(A)」の部分を虫めがねで覗いて見ましょう..どんな図が見えるでしょうか?
...
・図形全体と同様の線の並びが見えるでしょう!?
...
・では、思いきって倍率を上げて、電子顕微鏡で10万倍にして覗いて見ましょう!..
今度は何が見えると思いますか?
...
・答えは同じです..つまり、図2の図形は、どの部分をどう拡大しても、見える図形は、
全体の図形と同じ形をしているのです!
<線路の比喩>
・このような経験をしたことはないでしょうか..子供のころ、電車の一番前に乗って、
ずっと先まで伸びている線路を見ていた、なんて..
・その時見えた線路は先に行くほど幅が狭くなって見え、そのずっと先では「ほとんど
一点」にくっ付いているように見えます。
→その時、枕木は「図2」のように、先に行くほど、幅がだんだんと狭まって見え
ますよね。
…線路は、本当にくっ付いているんだろうか…
…あそこまで行ったら、どうなってるんだろう…
・1時間ほどその電車に乗っていたとしましょう..
前に「ほとんど一点」に見えていた所あたりまで、もう来たはずなんだけど、線路の
見え方には何の変化も見えない..
…やっとここまで来たのに…
…さっき(1時間前に)見えていた線路の景色と同じだ!?…
…今いる場所は確かに違うはずなのに、見える景色は同じだ!
…どうしてなんだろう?
1-2.フラクタルの樹
・下の図3〜5は「フラクタルの樹」です。この図の場合は、幹から枝を2本だし、そ
の枝が また二つに枝分かれしています。
→ 1本が2本 → 2本が4本 → 4本が8本 → 8本が16本
→ 16本が32本 → 32本が64本 → 64本が128本 → (ふうぅ..!)
・この図を描くために、初めてwindowsの「ペイント」を使いました。
・枝分かれする時、枝の長さは一定の比率で短くなり、枝の角度は一定であるものとし
て書かれています。(この図では約0.7倍)
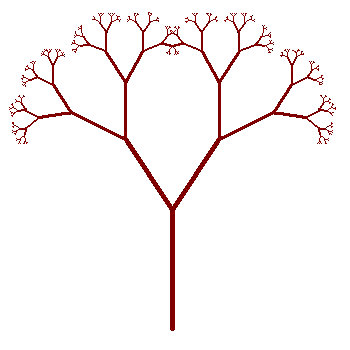 図3.フラクタルの樹−1
・図3の「フラクタルの樹」に葉っぱを書き加えてみたものが、次の図4です。どうで
しょう..少しは「樹」のように見えるでしょうか?
・この枝分かれの比率を徐々に変化させたり、枝分かれの角度や左右の枝の比率を変え
たりすることによって、自然界の植物の幹や葉の構造等々を単純な計算の繰り返しだ
けで、模写することができます。
図3.フラクタルの樹−1
・図3の「フラクタルの樹」に葉っぱを書き加えてみたものが、次の図4です。どうで
しょう..少しは「樹」のように見えるでしょうか?
・この枝分かれの比率を徐々に変化させたり、枝分かれの角度や左右の枝の比率を変え
たりすることによって、自然界の植物の幹や葉の構造等々を単純な計算の繰り返しだ
けで、模写することができます。
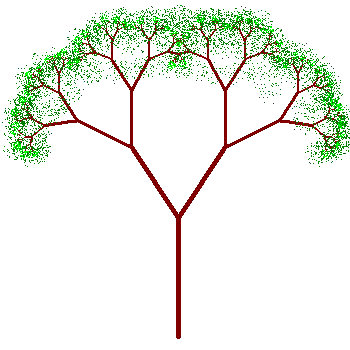 図4.フラクタルの樹−2
・では、この「フラクタルの樹」について説明します。
・図5をご覧下さい。この図は上の図と同じですが、各枝に番号が振ってあります。番
号は枝分かれの回数により、1番から9番まで振ってあります。
・9番目以上は図が小さくなりすぎてうまく描けないので、描いてないのですが、たと
え描いてあったとしても、もう見えませんね。
図4.フラクタルの樹−2
・では、この「フラクタルの樹」について説明します。
・図5をご覧下さい。この図は上の図と同じですが、各枝に番号が振ってあります。番
号は枝分かれの回数により、1番から9番まで振ってあります。
・9番目以上は図が小さくなりすぎてうまく描けないので、描いてないのですが、たと
え描いてあったとしても、もう見えませんね。
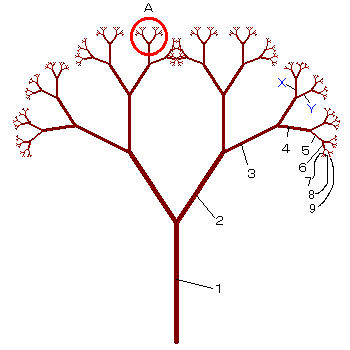 図5.フラクタルの樹−3
・この「樹」の場合も、図2の場合と同様に、「円A」の部分を拡大して
見ることにしましょう..何が見えるでしょうか?
...
・「円A」の内部を拡大しても、この図全体の図と同じ図形になることが想像できます
よね!?
・そうです。この フラクタルの樹 にも完全に自己相似性があるんです!
図5.フラクタルの樹−3
・この「樹」の場合も、図2の場合と同様に、「円A」の部分を拡大して
見ることにしましょう..何が見えるでしょうか?
...
・「円A」の内部を拡大しても、この図全体の図と同じ図形になることが想像できます
よね!?
・そうです。この フラクタルの樹 にも完全に自己相似性があるんです!
【 2.ラクタルの樹からの類推 】
2-1.フラクタルの樹に登ってみよう
さあ、それではこの樹を登ってみましょう!..とりあえず、私達は蟻にでもなったこ
とにしましょうか...
・まずは、枝(1=幹)を登ります..これには何も問題ないですね。
次は、枝(2) を登りましょう..私は「右の枝」に登ることにしますが、あなたはどっ
ちにしますか?..この場合は二つに一つの選択になります。
次は、第3の枝です..また、選択がでて来ました..今度はどうしましょうか?
...
・同様に第9の枝に行きつくまでには、次々と「選択」をしなければなりません。まあ
サイコロでも振って決めて下さい!
・このフラクタルの樹は物の分類に使えることが分りますね..例えば、まず、動物か動
物でないかとか、人か人でないかとか、男か女かとか、子供か大人かとか..ダンスが
好きか嫌いかとか、ラテンが好きかモダンが好きかとか、スローやクイックが踊れる
か踊れないかとか、競技会に出たいか出たくないかとか、プロかアマチュアかとか..
・通常、物事を分類するには、大分類→中分類→小分類→..と言う風に、まず大枠から
分類して行き、どんどん細かい差異に注目して行く、と言う手法をとります。従って、
細かい分類をするためには、その差異についての専門知識がないとできないことにな
るわけです。
…違いがわかる..
と言う宣伝が昔ありましたっけ。
2-2.フラクタル的人生論
蟻の気持は分りにくいので、私達の人生について考えて見ましょう。
・私達は生きていく過程で、目標に向かって努力をしたり、問題に直面して悩んだり、
歳を経てから昔の辛い経験を思い出して「あの時は辛かった」とか「でも楽しかった」
とか「若かった」とか、回想したりします。
・つまり私達は、それぞれ自分の「フラクタルの樹のような人生」を歩んでいるような
ものだと、お考え下さい。
一生懸命努力して、目標まで到達しようとする人、途中であっちこっちと色んな「枝」
に行って遊んでいる人..様々です。
2-3.大同小異
・政治的行動をしている人達は、確固たる主義主張をお持ちのようですが、たとえば、
自民党内部の派閥間の差異なんて、私達にはほとんど分らないし、反自民の人たちは
なんで大同団結して「反自民」でまとまれないんだろうなんて思ったりします。
・昔の学生運動では、「反帝国主義」等の目的では一致していたはずのに、内部では、
その「○○派」と「△△派」は「内ゲバ」と言う「ケンカ」を繰り返しやっていまし
た。
・これらについて、フラクタルの樹から類推して考えてみると..
・党派の外部に居る私達は、いわば「樹」の根っこ近くにいるのに対して、党派の内部
にいる彼らは、樹の「枝−X」とか「枝−Y」にいるように見えます。私達から見れ
ば、..
…「4番目の枝」までは一緒なんだから、ほとんど同じ考え方の人達じゃない
のか!?
…どうして一緒にやっていけないんだろう?
…「大同小異」だよ!
となります。
・しかし、実際に「5番目の枝」に居る彼らに見えている景色は、「円A部の拡大図は
全体と同じ」の通り..また、そこから先の目標は大きく異なっているので、彼らの考
え方の差異は大変大きいものとして見えてしまうのでしょう。
そう簡単には「大同団結」はできないのです。
では、どうしたらいいのか...
2-4.初心忘るべからず
・「初心忘るべからず」とは、「当初の志しを忘れるな」と言うことだと思うんですが、
「当初の志し」とは、その後知ることになる「技術論」や「専門知識」を持たない状
態で描いた目標..専門用語で語る目標ではなく、「誰もが分る言葉で語れる目標」の
ことだと思います。
・努力の結果、現在は「9番目の枝」にまで到達することができたとしても、常にその
位置から物事を見渡すのではなく...
…たまには、高みの枝から離れ、その根の位置に立って、物事を眺めてごらん
なさい!
…また、根の位置から見た自分の現在位置を確認しなさい!
2-5.問題は解決するか
ここに、ある経営者がいます。彼は、幾つかの会社運営上の悩みを持っていました。
・社内の業務分担等の体制を整えたいとか、社内伝票の流れをスムースにしたいとか、
優秀な人材を確保したいとか、売上を伸ばしたいとか...
努力の結果、彼は諸問題を解決し、売上も倍増したものと考えましょう。
・しかし、「自己相似性」の物の見方によれば、世の中そんなに甘くないことが分るで
しょう..即ち、
…以前あった問題は確かに解決したが、今度は、また別の問題が見えて来た。
…現在の業績を維持・拡大するために、以前同様の会社運営上の悩みを持つこ
とになり、ちっとも楽にはならない...
…しかも、問題の内容もより高度なものになってきた...
・「妥協」と言う言葉は、余りいい意味では使われないかも知れませんが、目標の完全
な達成があり得ないことを知れば、多かれ少なかれ「妥協」と言う言葉が暖かい言葉
に聞こえるはずです。
…細かいことには目をつぶれ
…「結婚したら両目をつぶれ」とは披露宴で言われる名文句!
・「常に努力を怠らず、常に上昇志向を持つ」ことは素晴らしいことですが、その時、
忘れちゃいけない言葉が「初心忘るべからず」かも...
・自分の位置を、その近くの「枝」に対する「相対的位置」としてばかり見るのではな
く、時々は「根」の位置に立ち、そこからの「絶対的位置」も確認することが重要な
ことなのでしょう。
2-6.ヘーゲルの弁証法 (2001.10.28)
・物の考え方の一つにヘーゲルが 150年ほど前に唱えた「弁証法」と言うものがありま
す。「正−反−合」という図式のアレです。
・その時点での正しい結論(正)があったとして、それと条件や立場の異なる見方から
の意見(反)が発生し、結論(正)とそれに対する反論(反)との両方を考慮に入れ
た「よりよい結論」(合)が新たに導き出されます。
・「合」と言う結論はその時点での「正」であり、「正」が確立されるとそれに対する
「反」がまた生まれ、また新しい「正−反−合」という関係が生まれ、..この関係が
際限なく繰り返される。..つまり「弁証法」の構造も無限なのです。
・私は哲学に詳しくないので、これ以上の深い考察はできませんが、ただ弁証法の構造
も自己相似性を持ったフラクタルなんだと言うことだけを付記しておきたいと思いま
す。
【 3.ディジタル的変化について 】
3-1.雪が積もり出す瞬間
・フラクタルの自己相似の話からは外れますが、ついでに、ディジタル系についても触
れてみたいと思います。
|
<雪のはなし>
私が小学生のころの話ですが、当地でも冬になると、時々雪が降りました。
私ばかりでなく、雪国ではない地域の子供達にとっては、雪は珍しいもので、
雪が積もったりすると、大人達にとっては、雪かきだ、雪下ろしだと、大変
厄介なものだなんてことはお構いなしで喜んだものです。
その日は午後から雪が降り出しました...
「雪だ〜」「積もらないかなあ」...
雪は積もるどころか、降っても降っても、無情にも片っ端から解けて消えて
しまいます。雪は夜になっても積もり出す気配はありませんでした。
「積もらないかなあ...」「せっかく降ってるのに...」
「みんな消えちゃうぅ...」
私はまた、「積もり出す瞬間」を目撃したかったのですが、結局、その日は
積もり出すところを目撃することはできず、寝ることにしました。
しかし、翌朝 目がさめて 外を見てみると、一面の銀世界になってました!
「雪が積もってる!」
…だけど、いつから積もり出したんだろう…
「積もり出す瞬間」を見たいと言う子供心は、「サンタクロースの正体」を
知りたいと言う子供心と同じようなものだと思います。
子供のころ、あなたも同じように思ったことはありませんでしたか?
|
|
・雪が積もり出す瞬間を見てみたいと言う思いは、私の場合はその後もずっと持ってい
ました。
・これが分るようになったのは、大学に入ってからのことでした。
・これはつまり「カタストロフィー」だってことがやっと分りました。
カタストロフィーと言うのは、ちょうど「ししおどし」がその竹筒に水がたまる
と、ある瞬間に水の重さで竹筒がひっくり返って、「コーン」と音がする。...
あるいは、犬が、敵が近づいて来ると「ウー」と言う低いうなり声を出し、その
「ウー」が昂じると今度は「ワン!」と吠える..と言うような「突然に出現する
現象」を取扱う学問です。
・雪の積もり出す瞬間は、次のようになります。
1)雪が降り出すと、地面に落ちたは雪は始めは解けてしまいますが、雪が解ける時、
実は、地面の熱を奪っているので、周りの水や地面の温度は、その分だけ下げら
れる。
2)その結果、目に見える変化は起きてないものの、実は地面の温度は確実に下がっ
て行き、ついには、雪を解かす温度以下になります。
3)そうなると、その後に降り続いた雪は、もう解けることなく「ずんずん積もる」。
ということになります。
3-2.努力の成果は目に見えない!
王子さまと友達になったキツネは、王子さまに秘密を教えます..
「かんじんなものは目に見えない」..
(『星の王子さま』 Saint Exupery)
・何事もそうだと思いますが、努力しても努力しても、自分には「努力の成果」はなか
なか見えてこないものだと思います。外国語の会話を習ったって「目に見えて」話せ
るようにはならないんです。
・あなたが、リズム感を身に付けようとして「マラカス」の練習を始めたとしても、そ
う簡単には「目に見えて」できるようにはならないのです!
・成果はなかなか目に見えるようにはならない..ここで諦めてしまう人は、結局はでき
ないままでおしまいですが、諦めずに努力を続けた人は、急に上手になるんです...
何故って、努力の成果は初めのうちは「目には見えない」ものなのですからね。
・しかし、目には見えてなくても、体の内部(脳や筋肉や神経系)には、努力した分が
ちゃんと記録されているんですよ!
・そしてある日、脳細胞にバラバラに記録されていた事柄が「サーッ」と脳の中でネッ
トワークのように繋がって来ると...
あ〜っ、わかった〜!
と言う感じになって..後はもう楽です。
→「その日」(雪が積もり出す瞬間) は突然にやって来る!!
☆デフォルト・モード・ネットワーク〜NHK「人体 神秘の巨大ネットワーク」より:
最新の科学では、この「わかった〜」や突然の「ひらめき」がどのように起こるのかが説明さ
れています。
・ぼーっとしている時の脳の状態を「デフォルト・モード・ネットワークと呼ぶのだそうですが、
これは「脳が何もしていない状態」の時のことで、「アルキメデスがお風呂に入っている時」
や「iPS細胞の山中教授がシャワーを浴びている時」がそうで、...
この時「大脳皮質に保管されている“記憶の断片”が自由自在に繋ぎ合わされ、新しい発想が
生み出される」のだそうです。
・ぼーっとしていれば誰にでも「ひらめき」が起こるかと言えば、そうではありません。その元
になる「記憶の断片」がなければ、何も繋げることはできません。いつもボーっと生きてると、
「チコちゃんに叱られる」かも...^^; ('19.01.03追記)
・「努力の第一段階」の終了です。
→いやいや、それからが大変なんだよ!だって、ほら、フラクタルの樹を思い出し
てごらんよ!
→そんなことを言われるとやる気がなくなっちゃうなあ...
→だから、「いい指導者」って言われる人は、教習課程をいくつかのステップに分
けて、そのステップ毎に、「その範囲での成果を目に見える」ようにしてくれて、
習う側の人がやる気をなくさないようにしてくれる、そんな先生のことを言うの
かなあ...
→それだけじゃないと思うけど、まあ重要な要素かも知れないね。
それに、内容の整理ができていて、ちゃんと説明ができないとね。
それに、「生徒の方がカシコイ」場合だって、あり得ることだから、先生自身も、
日々努力している人がいいよね...
・しかしながら、言うは易し、行うは 何とやら...
・さて、それでは、次は「2番目の枝」に挑戦しましょう!?
3-3.努力の成果は階段のように? '22.08.31追記
・努力の成果は、努力の量に正比例するのではなく、階段のようにディジタルに変化する
でしょう。
・レオンハルト・オイラーは「素数階段」の図を作ったとのことなので、私も99以下整数
について素数階段の図を描いてみました。
→横軸に整数を書き、その整数が素数だった場合は、1段上げて図を描きます。
→その後15歳の少年ガウスは対数曲線との類似性に気がつくことになります。
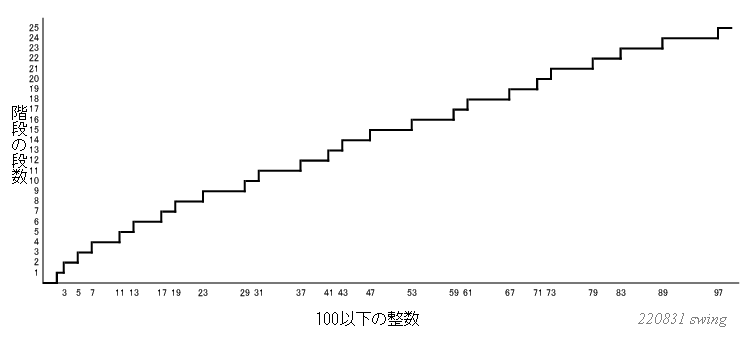 図6.素数階段
・努力は1段ステップアップするためには“それなりの努力”が必要ですが、素数階段は
単なる“図”なので、ステップアップのための努力やエネルギーは必要ありません。
もし、素数階段の段のステップアップにも何らかの努力やエネルギーが必要だとしたら、
リーマンのゼータ(ζ)関数が物理学と結びついて、面白いことになると思うのですが、
これは単なる私の夢想です。
図6.素数階段
・努力は1段ステップアップするためには“それなりの努力”が必要ですが、素数階段は
単なる“図”なので、ステップアップのための努力やエネルギーは必要ありません。
もし、素数階段の段のステップアップにも何らかの努力やエネルギーが必要だとしたら、
リーマンのゼータ(ζ)関数が物理学と結びついて、面白いことになると思うのですが、
これは単なる私の夢想です。






図2.一次元のフラクタル図形 ・この図には、縦線が何本か引いてありますが、左から右に行くに従って、その間隔が 一定の比率で狭まっています。(この図では約0.7倍) ・幅がどんどん狭まって行くと「円(A)」の中心部分あたりで、それ以上右には行けな くなる限界に行き着きます。 ・この「円(A)」の部分を虫めがねで覗いて見ましょう..どんな図が見えるでしょうか? ... ・図形全体と同様の線の並びが見えるでしょう!? ... ・では、思いきって倍率を上げて、電子顕微鏡で10万倍にして覗いて見ましょう!.. 今度は何が見えると思いますか? ... ・答えは同じです..つまり、図2の図形は、どの部分をどう拡大しても、見える図形は、 全体の図形と同じ形をしているのです! <線路の比喩> ・このような経験をしたことはないでしょうか..子供のころ、電車の一番前に乗って、 ずっと先まで伸びている線路を見ていた、なんて.. ・その時見えた線路は先に行くほど幅が狭くなって見え、そのずっと先では「ほとんど 一点」にくっ付いているように見えます。 →その時、枕木は「図2」のように、先に行くほど、幅がだんだんと狭まって見え ますよね。 …線路は、本当にくっ付いているんだろうか… …あそこまで行ったら、どうなってるんだろう… ・1時間ほどその電車に乗っていたとしましょう.. 前に「ほとんど一点」に見えていた所あたりまで、もう来たはずなんだけど、線路の 見え方には何の変化も見えない.. …やっとここまで来たのに… …さっき(1時間前に)見えていた線路の景色と同じだ!?… …今いる場所は確かに違うはずなのに、見える景色は同じだ! …どうしてなんだろう? 1-2.フラクタルの樹 ・下の図3〜5は「フラクタルの樹」です。この図の場合は、幹から枝を2本だし、そ の枝が また二つに枝分かれしています。 → 1本が2本 → 2本が4本 → 4本が8本 → 8本が16本 → 16本が32本 → 32本が64本 → 64本が128本 → (ふうぅ..!) ・この図を描くために、初めてwindowsの「ペイント」を使いました。 ・枝分かれする時、枝の長さは一定の比率で短くなり、枝の角度は一定であるものとし て書かれています。(この図では約0.7倍)
図3.フラクタルの樹−1 ・図3の「フラクタルの樹」に葉っぱを書き加えてみたものが、次の図4です。どうで しょう..少しは「樹」のように見えるでしょうか? ・この枝分かれの比率を徐々に変化させたり、枝分かれの角度や左右の枝の比率を変え たりすることによって、自然界の植物の幹や葉の構造等々を単純な計算の繰り返しだ けで、模写することができます。
図4.フラクタルの樹−2 ・では、この「フラクタルの樹」について説明します。 ・図5をご覧下さい。この図は上の図と同じですが、各枝に番号が振ってあります。番 号は枝分かれの回数により、1番から9番まで振ってあります。 ・9番目以上は図が小さくなりすぎてうまく描けないので、描いてないのですが、たと え描いてあったとしても、もう見えませんね。
図5.フラクタルの樹−3 ・この「樹」の場合も、図2の場合と同様に、「円A」の部分を拡大して 見ることにしましょう..何が見えるでしょうか? ... ・「円A」の内部を拡大しても、この図全体の図と同じ図形になることが想像できます よね!? ・そうです。この フラクタルの樹 にも完全に自己相似性があるんです!
 図6.素数階段
・努力は1段ステップアップするためには“それなりの努力”が必要ですが、素数階段は
単なる“図”なので、ステップアップのための努力やエネルギーは必要ありません。
もし、素数階段の段のステップアップにも何らかの努力やエネルギーが必要だとしたら、
リーマンのゼータ(ζ)関数が物理学と結びついて、面白いことになると思うのですが、
これは単なる私の夢想です。
図6.素数階段
・努力は1段ステップアップするためには“それなりの努力”が必要ですが、素数階段は
単なる“図”なので、ステップアップのための努力やエネルギーは必要ありません。
もし、素数階段の段のステップアップにも何らかの努力やエネルギーが必要だとしたら、
リーマンのゼータ(ζ)関数が物理学と結びついて、面白いことになると思うのですが、
これは単なる私の夢想です。