|
＜はじめに＞ 同じ標準MIDI（GM）データを演奏しても，音源によっては，聞こえ方が全く違うこともしばしばです。ここでは，ベロシティー（その音の大きさを示すパラメータで，1-127の値を指定できる，以下 vel. と表す）の値と実際の音の大きさの関係，また，それが音源の種類によってどう違うか，を調査してみました。 なお，ここでは音の種類を示す「プログラムチェンジ（以下p.c.と略する）」の値を，0-127の値を取るものとして扱います。 ＜今回調べた音色グループ＞
音源の設定の条件はすべての音源について， ＋ （各種リセット[GS，XG，GM]） ＋ （ボリューム 127） ＋ （プログラムチェンジ [音の種類に対応したそれぞれの値]） ＋ （パン 127［めいっぱい右］） ＋ （デジタル効果[リバーブ，コーラスなど]なし） としました。 また，ベロシティーを変化させたときの音量の変化を調べるため， ＋ （ゲートタイム：Ｔg（音の種類による）） ＋ （空き時間：Ｔbl1（音の種類による）） ＋ （コントロールチェンジ[c.c.]120-値-0） ＜オールサウンドオフ＞ ＋ （空き時間：Ｔbl2（音の種類による）） の「命令」を，ベロシティーを変化させながら繰り返したものをMIDI音源で発音させ，その音を数値データとして取り込みました。ただし，MU90B では「オールサウンドオフ」が利かないことがたびたびありました。（ここで測定したベロシティーの値：vel.= 1，5，10，15，……，115，120，125，127）  なお音源本体のボリュームは，音源本体ごとに常に一定（最大）にしました。また「ノートナンバー69」の音は右図に相当し，440 Hz の周波数です。 発音された音の波形のデータは，各音源のラインアウト端子のR（右）からの出力に 47 kΩ の抵抗をつなげたときの抵抗の両端の電圧をアナログ／デジタル（A/D）変換器を通してノートパソコンに取り込むことによって得ました。（ A/D変換器とノートパソコンは，研究室（１）と同じものです。ただし，A/D変換器のサンプリング周波数は 16.6…kHz。） ＜結果＞ まず，各ベロシティーに対する音の大きさをどういうものの数値で表すか，というのが問題になりますが，ここでは簡略のため，音の波形グラフの振れ幅（最大と最小との差）の1/2の電圧値を「振幅」とし，GZ-50M以外ではそれを使うことにしました。（音の波形グラフのようすは，研究室（2）などを参照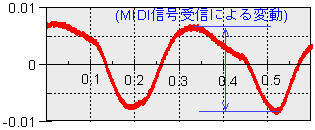）  GZ-50Mでは，上記の「振幅」に若干の修正を加えました。右図は，ピアノ[p.c.0]でベロシティーの値が1のものの波形データを示したものです。ここでは，縦軸は電圧[V]，横軸はグラフ上での相対時刻[秒]，を表しています。この図のような「変動」は，どのベロシティーの値でも起こっているので，これは，MIDI信号を受信した時に発生すると思われます。また，この「変動」はそのときごとに，形や大きさが多少変化します。このため，GZ-50Mでは「振幅」を修正するために，以下の手順に従いました。
実際に耳が感じるのは「エネルギー」だから，単位時間に耳が感じる「エネルギー」Ｉ は，単一周波数成分のみでは， と考えられます。ただし，＾2は2乗，∝は比例，V は音源の出力電圧，R は負荷抵抗を表します。したがって，音の周波数成分が同じであるとき，近似的に， と考えられます。この両辺の対数を取って整理すると， したがって，「振幅」の対数で考えれば，それは，実際に聞こえる大きさを考えることになります。 上のことは，あくまでも「荒っぽい」近似です。なぜなら，同じ振幅でも周波数によって「耳の感度」は違いますし，同じ音の高さ（ノートナンバー）でも，ベロシティーの値によって，音源から発生する音の音質が変化（周波数成分が変化）することがあるからです。 とは言っても，大まかな傾向は十分に分かると思います。 具体的な，音の種類[p.c.]ごとの結果を，次の別ページに記載します。なお，各[p.c.]共通の説明については，ピアノ[0]にのみ書かれてありますので，必ず ピアノ[0] を先にお読み下さい。（（ ）内はページの内容のサイズ）
（上記の結果をより実用的にまとめたグラフ集は，こちらへどうぞ。） なお，音の種類[p.c.]による違いの考察は，別の機会に行う予定です。 |